MODELER is an automated protein homology modeling package that builds a 3D model of a protein sequence using data from the alignment of the sequence with one or more homologous structures.
Sali, A. Blundell, T. L., "Definition of general topological equivalence in protein structures: A procedure involving comparison of properties and relationships through simulated annealing and dynamic programming," J. Mol. Biol., 212 403-428 (1990).
Sali, A. and Blundell, T. L., "Comparative protein modeling by satisfaction of spatial restraints, Movl. Biol., 234 779-815 (1993).
Sali, A., Matsumoto, R., McNeil, H. P., Karplus, M., and Stevens, R. L., "Three-dimensional models of four mouse mast cell chymases. Identification of proteoglycan-binding regions and protease-specific antigenic epitopes," J. Biol. Chem., 268 9023-9034 (1993).
Sali, A and Overington, J.P.,"Derivation of rules for comparative protein modeling from a database of protein structure alignments," Protein Sci., 31 582-1596 (1994).
MODELER derives spatial restraints such as inter-Ca distances and dihedral angles from each homologous structure. The weight assigned to the derived restraints reflect the degree of local sequence similarity between the homolog and the model sequence. The restraints are expressed as probability density functions (pdfs) that describe a model structure. The model is derived by minimizing violations of the restraints. The optimization process to generate the model consists of applying the variable target function as well as conjugate gradients and running molecular dynamics.
The MODELER program was developed by Dr. Andrej Sali at Birkbeck College (London), Imperial Cancer Research Fund (London) and Harvard University. It is described in detail in papers listed in the references section.1-4
QUANTA provides a simple interface that you can use to set up and run a MODELER job. The jobs typically take between five minutes and several hours to run so they are generally run in the background. Model structures generated from a MODELER run can be read back into QUANTA for display.
This chapter describes the QUANTA/MODELER interface, steps to take to use MODELER from within QUANTA, and functionality that you can access. It covers the following areas:
You can access MODELER functionality that is not currently interfaced with QUANTA by editing the control file generated within QUANTA and then running a MODELER job. The full MODELER functionality and interface is described in the MODELER User's Guide and Programmer's Manual. This book is available on-line as a postscript file in the following location:
$MODELLER_ROOT/doc/manual.ps.Z
The tools to Run MODELER and Read MODELER Results are available in the Protein Design application. These tools and additional tools to analyze the MODELER results are available in the Protein MODELER application.
Before running MODELER, you should align and superpose the sequence and homologous structures using the Align and Superpose utility which is available in either the Protein Design or Protein MODELER application within QUANTA. For more information, see Chapter 5. Alternatively alignments generated outside QUANTA can be read in using the Sequence utility on the Files pulldown and selecting Read Sequence/Alignment File. You will have the option to read alignment files in several commonly used formats.
MODELER does not require multiple homologous structures to be superposed. However, superposition may help you in studying the structures. In contrast, the alignment of the structures is the most significant input to MODELER. If there is any uncertainty in the alignment of the sequences you are studying, it is worth your time to try all alignment possibilities. You can improve alignment decisions by checking the final pdf value of each MODELER run to determine the residues that have poor restraint satisfaction, then adjusting the alignment accordingly.
You can use fragments to model limited segments of structures by aligning the fragment to the appropriate part of the model sequence. This process can be useful if a motif from a non-homologous structure is a good analogue for part of the model.
You can build models in the presence of ligands or prosthetic groups but this requires manual generation of restraints to position the ligand.
1. Select Applications from the main menu, then select Protein MODELER from the Applications pulldown. The Protein MODELER and Protein Utilities palettes are displayed.
2. Select Run Modeler in the Protein Design palette. A dialog box is displayed.
3. Specify run parameters as described in the following paragraphs:
Currently active sequences are listed near the top of the dialog box. Choose one of these as the sequence for which a model will be built.
This sequence can come from either an MSF file or a sequence file. If there are already coordinates for the sequence, they will be completely ignored by the interface. All other active molecules will be used as homologues for the model.
The name should be unique because it will be used as the root name for files and a directory created in running the MODELER job. If the name is not unique, you will be prompted to enter an alternative.
By default, MODELER will build one model, but multiple models can be generated.
An initial model is generated by copying and averaging the homologs. Multiple models are generated by perturbing this initial template to generate models with a given RMS deviation in coordinates. All models are then refined independently. Their structures may converge or diverge.
Most of the time required for a MODELER run is used in optimizing the structure. The optimization protocol involves multiple cycles of refining the model coordinates as the scaling of the restraint parameters is gradually varied to bring in tighter restraints. Available optimization protocols are:
Full - Optimization using copying and averaging of template coordinates, variable target function with conjugate gradients, and molecular dynamics with simulated annealing. Full is the default and recommended selection.
Partial - Optimization using copying and averaging the template coordinates plus variable target function with conjugate gradients.
None - No optimization. Copying and averaging the template coordinates only.
By default, a MODELER job starts automatically in background mode on your local host You can change this by checking the appropriate box:
Prepare control file only; do not run MODELER.
The MODELER control file, input alignment file, and PDB coordinate files are always written. If you want to modify the control file before running the job, choose this option, edit the control file, then run the job outside QUANTA by entering the command:
modeler model_name
When you check this box, a Select Host dialog box is displayed. For more information, see "Using External Applications" in QUANTA Generating and Displaying Molecules.
MODELER jobs take between five minutes and several hours. Job time increases with the size of the protein and the number of homologs.
To check if a MODELER job is complete, select Show Status in the Calculate pulldown.
After a MODELER job is run, you can display the models within QUANTA.
1. Select Display MODELER Results... in the Protein MODELER palette. A File Librarian listing the MODELER control (.top) files is then displayed.
2. Select a MODELER control file (model_name.top). QUANTA reads the log file associated with this job to check that the job has run successfully and then reads in the output model files for this job from model_name_dir/model_name.B9999nn.pdb. and creates MSF files with the file names model_name_nn.msf. The nn designation is an incremental number for each model. This number is 01 if there is only one model.
3. Click open. The model structures are displayed in the molecule window. The sequence of the model structures is automatically aligned to the input homologs for the model if they are still selected within QUANTA. Models in MSF files can be manipulated in QUANTA like any other MSF files. The final pdf for the model is listed in the textport.
MODELER generates a large number of restraints to force a model towards the structure of the homolog(s) and to maintain good structure geometry. At the end of a MODELER refinement not all restraints will have been satisfied and the violations associated with each residue can be summed to give an indication of the quality of the model in and around that residue. There is not a simple interpretation of the absolute value of the restraint violation parameter since parts of a model, for example residues adjacent to an insertion or deletion, are almost certain to have higher restraint violations. The violations are useful in making comparisons between different models. Models with lower violations in a region are probably better in that region. If these models have been generated from different initial alignments of the model sequence and the homologs, then lower restraint violations are a strong indication of better alignment.
In the PDB files output by MODELER the residue restraint violation is listed in the place of the temperature factor parameter. In an MSF file, this information is stored as the fourth parameter (that is, BVALUE).
When the Display MODELER Results tool is used the restraint violations are shown as a graph in the sequence viewer. To redisplay the graph use the Plot Violations tool.
You can use the Color Violations tool to color the molecule and sequence by the violation parameters. The violation values are split into four ranges between the maximum and the minimum values observed for all the residues in the active molecules. The residues are colored white, pale yellow, yellow and red for increasing violations. The Legend tool on the Protein Utilities palette can be used to display a legend with the key to the color coding.
You can list the restraint violations for each residue by selecting the Ca atoms, then typing:
LIST ATOM
in the command line. The restraint violations are listed in the textport in the column labeled 4th.
The tools in Protein Health can be used to indicate improbable features in a model. Protein health exceptions, such as a residue main chain not in a regularly observed conformation or buried polar atom which are not hydrogen bonded, may be indicative of a poor model which, in turn, may indicate a poor choice of homologies or poor alignment. The Protein Health tools can be applied to the MSF files generated by the Read MODELER Results tool. If you have several MODELER models it may be easier to write them all to one CSR file using the Write CSR File tool and then using the Tabulate MultiConformations tool within Protein Health to produce a table which summarizes health exceptions for all of the models (see chapter 19.).
Profile analysis can be applied to the models generated by MODELER and will plot graphs of scores per residue in the sequence viewer which aid comparison of the quality of models (see Chapter 1.).
When you begin a MODELER job, a directory is created below your current working directory and all files related to the job are placed there except the control and log files.
The name of this directory the same as the name of the control file except for extensions. Models generated by MODELER are placed in this directory. Generally, you will read these files through the QUANTA interface.
When you have finished a MODELER run, after the final model .pdb files have been read and MSF files have been generated in QUANTA, you can delete the job directory.
Type the following on the command line:
sys rm -rt directory_name
This will remove the directory and the MODELER files in it.
This section provides information on the files used by QUANTA in running MODELER. None of this information is necessary for you to use MODELER from the QUANTA interface.
When a MODELER job is started, the following files and directory are created by QUANTA:
MODELER creates the following files:
Column 1 - An index to the schedule step.
Column 2 - Optimization method (1=CG, 2=Newton Raphson 3=MD).
Column 3 - For the variable target function method restraints, the maximum number of residues and the span of the restraints.
Column 4 and beyond - Scaling factors for the standard deviations of restraints, one column per physical restraint type. The types are listed in $MODELER_ROOT/modlib/feats.lib (currently, 1-24 types).
MODELER works as a command interpreter for a command language called TOPS. The TOPS language is similar to FORTRAN and includes commands to define variables, open and close files, call subroutines, and do some flow control.
The language is described in Chapter 3 of the MODELER User's Guide and Programmer's Manual. A MODELER command file is written in the TOPS language and only when a valid MODELER command is recognized by TOPS is the appropriate MODELER function run. The TOPS language provides the framework for flow control for running MODELER.
MODELER commands are described fully in Chapter 2 of the MODELER User's Guide and Programmer's Manual along with the keywords that allow you to change the parameters for the commands. A full list of commands and keywords is in the file $MODELER_ROOT/modlib/top1.ini. This file is read every time MODELER is run.
A complete MODELER run requires a lengthy command script. Scripts to perform common functions are provided in the $MODELER_ROOT/exec directory.
A simple MODELER control file for homology modeling consists of commands to specify the input files and set any non-default parameters, and to then call the homol subroutine that controls the model building procedure. For example, the control file written by QUANTA to build a model named dfr_model from two structures, 3dfr and 4dfr is set up in the following form:
INCLUDE
Set the MODELER working directory for input, coordinate and output files:
SET DIRECTORY = `dfr_model_dir'
SET ATOM_FILES_DIRECTORY = `dfr_model_dir'
SET OUTPUT_DIRECTORY = `dfr_model_dir'
Set an extension PDB for the output coordinate files:
SET PDB_EXT = `.pdb'
Set the format for the input alignment file to QUANTA format and specify the alignment file:
SET ALIGNMENT_FORMAT = `QUANTA'
SET ALNFILE = `dfr_model.aln'
Declare the sequence for which to build models. The sequence is taken from the alignment file and no further information is needed:
SET SEQUENCE = `dfr_model'
Declare what molecules in the alignment file are homologues of a known structure. The molecule names must correspond to those in the alignment file. There should be .pdb coordinate files with the corresponding molecule_name.pdb:
SET KNOWNS = `3dfr' `4dfr'
Next is a comment line which is not interpreted by MODELER. It is read by QUANTA and used to put the model in the correct sequence alignment to the homologous structures:
# QUANTA input sequence = dfr.msf
Set the optimization protocol:
SET MD_LEVEL = `refine3'
Call the main MODELER script from $MODELER_ROOT/exec to control the program flow:
CALL ROUTINE = `model'
This section describes several file modifications, including adding a disulfide bond and representing hydrogens, that you can make if you want to modify the models that MODELER generates These modifications are not required to complete a MODELER run.
If the target sequence has a pair of cysteine residues aligned to a pair of cysteine residues that form a disulfide bridge in any of the homologous structures, then a disulfide bond will be expected in the model structure and the necessary constraints will be defined automatically. Anticipated disulfide bonds are reported in the log file.
However, if you expect a disulfide bond in the model structure without an analogous bond in the homologous structures, then you must specify this bond in the control file for the necessary constraints to be set up.
MODELER control scripts include a dummy routine called special_patches that contains nothing. You redefine this routine to contain the information needed by MODELER to generate a disulfide bond.
To redefine the routine, edit the control file to include the following lines after the first INCLUDE statement:
SUBROUTINE ROUTINE = `special_patches'
PATCH RESIDUE_TYPE = `DISU', RESIDUE_IDS = n1 n2
RETURN
END_SUBROUTINE
where n1 and n2 are the index number of the disulfide bonded residues. Note that the index number is not necessarily the same as the residue ID unless the residues are numbered consecutively from 1 for the first residue.
By default, MODELER generates models without hydrogen atoms. By using alternative topology library models, you can generate models with polar hydrogens or all hydrogens.
The default topology is set in the file $MODELLER_ROOT/exec/__defs.top. This file can be edited to change the default.
Alternatively the following lines can be edited into the control file to setup the addition of polar hydrogens
SET HYDROGEN_IO = `ON'
SET TOPLIB = `${LIB}/top_polh.lib'
SET TOPOLOGY_MODEL = 2
SET PARLIB = `${LIB}/par.lib'
Or, to use an all-hydrogen representation, edit the control file:
SET HYDROGEN_IO = `ON'
SET TOPLIB = `${LIB}/top_allh.lib'
SET TOPOLOGY_MODEL = 1
SET PARLIB = `${LIB}/par.lib'
MODELER will generate models for multi-segment (i.e., multi-chain) proteins without any user intervention if the input alignment file has the segment delimiters, "/". The alignment files generated by QUANTA will have the segment delimiters for sequences taken from MSF files but since the QUANTA sequence-only data has no segment information there will be no segment delimiters in the alignment file. If your model structure is a multiple segment protein and its sequence is s in the form of sequence-only data then you should do one of two things:
The CHARMm Constraints Editor within QUANTA can be used to define MODELER restraints and write out an appropriately formatted file or to convert NOE information to MODELER restraint file format.
The appropriate tools can be accessed using Constraints Options and Dihedral/Distance in the CHARMm pulldown. The module includes options to import various constraint formats and to enter constraints by selection and editing the constraint table.
The MODELER restraint file format is described in the MODELER User Guide. Note that the MODELER restraint file references atoms by their number rather than by an atom and residue name and it is therefore very important to generate the restraint file for the correct molecular structure. The simplest way to ensure that the structure is correct is to run MODELER with the Optimization level set to None so that an initial model is generated but a full refinement is not performed. The initial model will be in the MODELER work directory with the name model_name_dir/model_name.ini and is in PDB format. This file should be read into QUANTA and used in the Constraint Editor.
In the MODELER restraint file the magnitude of a restraint is specified by the standard deviation in angstroms or radians (SD). This is different from the Charmm convention of specifying a force constant k. The relation between these is:
When exporting MODELER restraint files from the Constraint Editor, the necessary conversion is made from the force constant k to the standard deviation assuming a temperature of 297.15 K.
Dihedral constraints are defined in the MODELER restraint file as single Gaussian harmonic potentials and the target parameter in the Constraint Editor is taken as the ideal value. NOE distance constraints are interpreted in the MODELER restraint format as two restraints: one for upper and one for lower distance bound. The upper and lower bound distances reported in the Constraints Editor table, and not the target value, are used in defining the MODELER restraints.
Once a file containing user defined restraints is created and named, for example, user_defined.rsr can be read by MODELER by inserting the following lines in the control file generated by Quanta after the first line:
special_restraints is a subroutine which is called at those places in the modeler protocol where restraints are set up. By default, the subroutine contains no functionality but you can redefine the subroutine to incorporate such functionality as reading an additional restraints file.
If MODELER is used to build a protein model containing a ligand, then the ligand is treated as a rigid body. Its conformation is fixed but the position relative to the protein may alter. To anchor the ligand in the correct position distance restraints between ligand and protein atoms can be defined using the protocol outlined above.
Protein and nucleic acid sequence determination is now routine in molecular biology laboratories. As a result, the rate of publication of sequence information has increased dramatically. Several organizations have compiled databases to centralize the published information and to facilitate its use in research (EMBL database, PIR/NBRF database, GenBank database). On the other hand, structural information from X-Ray crystallographic or NMR results is obtained much more slowly. For instance, if the protein is not a simple mutation of one whose structure is already known, it can take months or years to perform a complete structural determination. Because of the disparate rates of sequence and structure determination, there are many proteins for which sequence information is known but the 3D structure is not.
It is advantageous to have a method whereby the conformation of a newly characterized protein can be predicted from its amino acid sequence.1 The importance of homology modeling is drastically increased with the explosive multiplication of completely sequenced genomes and parallel structural databases of models based on these genomes.
Early work dealing with building a protein by homology used only one known structure (Browne et al. 1969, Shotton and Watson 1970). Amino acid similarities between the known and unknown proteins were used to determine where one protein would resemble the other. Sequence alignment was done, and the coordinates of the reference protein were used to predict those of the unknown protein.
More structural approaches have been suggested by Greer and Blundell (Greer 1980, 1981, 1985; Blundell 1987, 1988). In their methods, more than one reference protein is used, and a greater emphasis is placed on the conformational similarities between them. Less emphasis is placed on sequence alignment alone as a basis for the model. By determining which portions of the molecules do not vary from one member of a protein family to another, there is greater confidence that extrapolation to a new member will be accurate.
While several reference structures are used in the traditional homology model building process, only one set of coordinates can be used in any one peptide segment. MODELER is able to simultaneously incorporate structural data from one or more reference proteins. Structural features in the reference proteins are used to derive spatial restraints which in turn are used to generate model protein structures using conjugate gradient and simulated annealing optimization procedures.
Sequence-structure alignment (Align2D)
Structure alignment (Align3D)
Building the structure
Atom-atom repulsions
Distance between two Ca atoms
Distance between main-chain N and O atoms
Distances between sidechain-sidechain and sidechain-mainchain atoms
Main-chain conformation
Side-chain conformation restraints
Restraining Chi1 side-chain dihedral angles
Restraining Chi2 dihedral angles
Restraining Chi3 dihedral angles
Restraining Chi4 dihedral angles
Basis and feature probability density functions
Feature PDFs used for restraining model protein features
Structure generation using MODELER
Modeling loops
References
One of the main problems in comparative modeling is the accuracy of the sequence alignment. MODELER extends the global alignment algorithm to align two blocks of sequences (the structure block and the sequence block). The command uses a variable gap-opening penalty which depends on the 3D structure of the sequences in the structure block and tends to place gaps in a better structural context. The variable gap penalty favors gaps in exposed regions, avoids gaps within secondary structure elements, favors gaps after curved parts of the main-chain, and minimizes the distance between the two positions spanning a gap.
The sequences within the two blocks, structure block (first block) and sequence block (second block) should be prealigned and the first block is required to have at least one sequence with known 3D structure. The two blocks of sequences are defined in the MODELER control file as sequences 1 to ALIGN_BLOCK and ALIGN_BLOCK+1 to the last sequence.
The linear gap penalty function for inserting a gap in block 1 of a structure is:
| Eq. 4 |
|
where u and v are the usual gap opening and extension penalties (defined by GAP_PENALTIES_1D) and l is the gap length.
f1 in the above equation is a function that is at least 1 but can be larger to make gap opening more difficult, as in the following circumstances.
Between two consecutive (i.e., i, i+1):
The function represented by f1 is:
| Eq. 5 |
|
The weights, w, are the first four numbers in variable GAP_ PENALTIES_2D.
Hi is the fraction of helical residues at position i in block 1.
Si is the fraction of b-strand residues at position i in block 1.
Bi is the average relative side-chain "buriedness" of residues at position i in block 1.
Ci is the average straightness of residues at position i in block 1.
The original straightness is modified here by assigning a maximal straightness of 1 to all residues in a helix or b-strand.
The linear gap penalty function for opening a gap in block 2 (sequence block) is:
| Eq. 6 |
|
f2 in the above equation is a function that is at least 1 but can be larger to make the gap opening in block 2 more difficult, as in the following circumstances:
1. When the first gap position is aligned with:
2. When the whole gap in block 2 is spanned by two residues in block 1 that are far apart in space.
The function represented by f2 in the above equation is:
| Eq. 7 |
|
Hi is the fraction of helical residues at position i in block 1.
Si is the fraction of b-strand residues at position i in block 1.
Bi is the average relative side-chain "buriedness" of residues at position i in block 1.
Ci is the average straightness of residues at position i in block 1.
d is the distance between the two Ca atoms spanning the gap, averaged over all structures in block 1.
do is a distance small enough to correspond to no increase in the opening gap penalty (e.g., 6 Å).
Parameters wH, wS, wB, wC, wD, and do are specified by GAP_PENALTIES_2D.
For an example, see the standalone Modeler manual at:
http://salilab.org/modeller/manual/
Multiple templates are often used together to model a sequence. The Align_Structure command aligns two or more template structures based on their structural similarity. The command first generates a multiple sequence alignment using the progressive pairwise sequence alignment method. Based on the initial sequence alignment, MODELER performs an iterative least-squares superposition of 3D structures. This results in a new multiple structure alignment.
Starting from the initial sequence alignment, the structure alignment involves several cycles, each consisting of an update of the framework and calculation of the new alignment. The new alignment is based on superposition of the structures onto the latest framework. The framework in each cycle is obtained as follows.
1. The initial framework consists of Ca atoms in structure 1, but only at the alignment positions where all the structures have a residue. If there is a missing Ca atom in any of the residues at a given position, the coordinates for this framework position are approximated by the neighboring coordinates.
2. All other structures are fit to this framework. The final framework for the current cycle is then obtained as an average of all the structures, in their fitted orientations, but only for residue positions that are common to all of them, given the current alignment.
Another result is that all the structures are now superimposed on this framework. Note that the alignment has not been changed yet.
3. The multiple alignment itself is re-derived in N-1 dynamic programming runs, where N is the number of structures. This is done as follows.
a. Structure 2 is aligned with structure 1, using the intermolecular atom-atom distance matrix, for all Ca atoms, as the weight matrix for the dynamic programming run. The dynamic programming is the same as pairwise sequence alignment, where the sequence similarity matrix is replaced by the Ca distance matrix.
b. Structure 3 is aligned with an average of structures 1 and 2, using the same dynamic programming technique.
c. Structure 4 is then aligned with an average of structures 1-3, and so on.
Averages of structures 1-i (i=2,3,...n) are calculated for all alignment positions where there is at least one residue in any of the structures 1-i (i=2,3,...n). (This is different from a framework which requires that residues from all structures be present.)
Note that in this step, residues out of the current framework may become aligned and the current framework residues may become unaligned. Thus, after the series of N-1 dynamic programming runs, a new multiple alignment is obtained. This is then used in the next cycle to obtain the next framework and the next alignment.
The cycles are repeated until there is no change in the number of equivalent positions. This procedure is best viewed as a way to determine the framework regions, not the whole alignment.
Probability density functions
"Probability density functions observed in known protein structures
Probability density functions for bond lengths, bond angles, and dihedrals
In many areas of molecular modeling, geometric features such as distances and dihedral angles may be restrained by setting lower and upper bounds on their allowed values. A pseudo-energy term and a restraining force are then applied if the geometric feature in a model molecule is found to be outside of these bounds. MODELER describes restraints on such geometric features in terms of a probability density function (or PDF) p(c), for a feature c that is to be restrained. The area under the curve p(c) between c1 and c2:
| Eq. 8 |
|
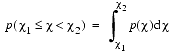
is the probability of an event in which c is observed within this range. This must integrate to one over the range of all possible values for the feature c. This description is more complete than the use of mean values and/or lower and upper bounds as a description for restraints.
In addition, the concept of a conditional probability density function is important in comparative modeling. The PDF used to restrain a geometric feature c can be written as
| Eq. 9 |
|
This describes the probability density for c when the other features a,b,c.... are specified. As an example, p(c1/ residue_type,f,y) could be used to describe the side-chain dihedral angle c1 for a known residue type and main-chain dihedral angles f and y.
The probability density functions used by MODELER are derived analytically using statistical mechanics and empirically using a database of known protein structures. Stereochemical restraints such as bond lengths, bond angles, dihedral angles, van der Waals repulsions, and disulfide bonds are derived from published parameters for a molecular mechanics forcefield (Brooks et al. 1983). The disulfide bond is restrained by distances, angles, and the C-S-S-C dihedral angle. Restraints such as those applied to Ca-Ca distances, N-O distances for main-chain atoms, main-chain dihedral, and side-chain dihedral angle classes are derived empirically from a database of known homologous proteins and their structural alignments.
The method of deriving PDFs from the database of known proteins may be found in Sali and Overington 1994. The database and PDFs depending on it are regularly updated (the last update was July, 1998).
The database is considered a representative sample of globular proteins and is suitable for deriving the relationships between features of protein structures. These relationships are expressed as PDFs. Features are derived at several levels. There are residue-residue relationships such as Ca-Ca distances, protein-protein relationships such as percentage sequence identity, residue properties such as solvent accessibility, and protein properties such as resolution in X-Ray diffraction.
Given the database of proteins, an analysis program is used to derive a table Wc,a,b,..c that approximates
:
| Eq. 10 |
|
This table contains the observed relative frequencies for a feature c given a,b...c. Non-linear least squares regression is then used to derive an analytic function that fits the table W.
| Eq. 11 |
|
where q represents a vector of non-linear fitting parameters. The forms of the probability density function derived for various geometric features used by MODELER are described below.
A classical harmonic oscillator model for a bond of equilibrium length 
leads to an energy expression of the form (Sali and Blundell 1993a):
| Eq. 12 |
|
where c is a constant for a given bond type. The probability density function for the bond length is then a Gaussian function:
| Eq. 13 |
|
where 
is a standard deviation and only two parameters,
and 
, are needed to describe this distribution. This functional form is monomodal having a single maximum at b =
.
The probability density function used to describe a bond angle a is analogous to that described above. The restraint is again a single Gaussian function:
| Eq. 14 |
|
The monomodal PDF for a torsion or an improper dihedral g is
| Eq. 15 |
|
This form is used in MODELER to restrain peptide and ring planarities as well as the chiralities of Ca atoms and Thr and Ile side-chains. To allow for the cis-peptide conformation, the main-chain dihedral w is restrained to a sum of two Gaussian functions, one centered at 0° and the other at 180°.
| Eq. 16 |
|
where w1 and w2 are fractional weights and their sum equals one. In general terms, a PDF for a bond length, angle, or dihedral f would be described by a functional form (Sali and Blundell 1993a):
| Eq. 17 |
|
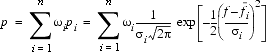
The mean values and standard deviations used for bond lengths, bond angles, and dihedral angles were obtained from the CHARMM22 parameter set (Brooks et al. 1983, Nilsson and Karplus 1986).
The atom-atom repulsion is not described by a harmonic model but uses a PDF of the form:
| Eq. 18 |
|
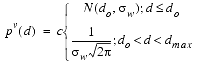
where d is the distance between the two atoms, do is the sum of their van der Waals radii, sw is the standard deviation part of the PDF (typically 0.05 Å), and dmax is the maximum possible linear dimension for a protein. The constant c is chosen so that this function integrates to 1. This form is flat for distances greater than do but presents a soft sphere repulsion for atoms closer than distance do.
The unknown feature used by MODELER is the difference between two equivalent Ca-Ca distances, or d'-d where d' is a Ca-Ca distance in the reference protein and d is that in the model structure. The database of known protein structures is used to find the distribution of d'-d as a function of four variables.
1. The corresponding Ca-Ca distance (d') in the known structure.
2. The fractional sequence identity (i) of the two aligned sequences.
3.
The average of the fractional solvent accessibilities (
) of the two residues spanning d' in the known protein structure.
4.
The average distance from a gap (
) of the residues spanning the distance d.
The database and the associated software were used to show that the Ca-Cadistance difference (d'-d) can be approximately modeled as a Gaussian function with a mean of zero and a standard deviation 
that depends upon the values of the four independent variables.
The form of the expression describing
is a cubic polynomial in the four variables 
:
| Eq. 19 |
|
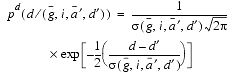
Using the protein database to extract values for
in the discrete ranges shown in Table 10 allowed the derivation of distribution histograms describing the variation of d'-d for various values of each of the four variables. The coefficients of the polynomial used to describe
were obtained by least squares fitting to the distribution histograms. The final form obtained is:
| Eq. 20 |
|
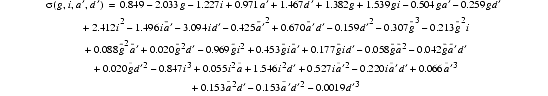
Examples of these Ca-Ca distance difference histograms and PDFs are shown in Figure 1.
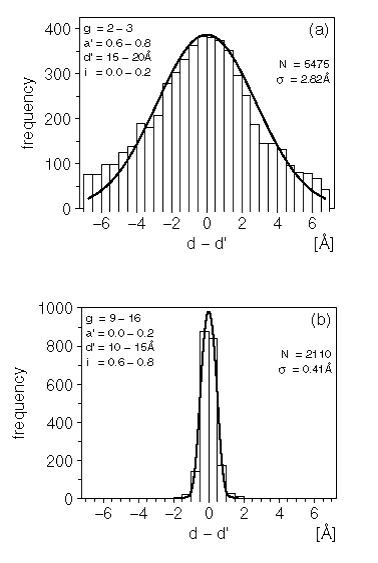
Figure 1. Distribution of the differences between 2 equivalent distances
The histograms show the frequency of the difference between 2 equivalent distances as observed in the alignments database. The curves are least-squares fits obtained as described in the text.
Another main-chain distance constraint is set for N-O atom pairs. The N-N and O-O distances are not constrained. The N-O distance (h) in the model protein is again described by a Gaussian distribution describing the difference between h and the corresponding distance h' in a known structure.
| Eq. 21 |
|
The expression for 
is again a cubic polynomial in these four variables. The coefficients were derived in a manner similar to that just described for the Ca-Ca distances. The final form obtained for
is
| Eq. 22 |
|
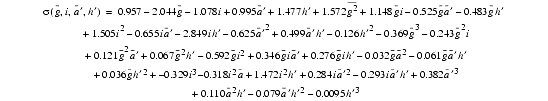
If the model protein contains sidechain-sidechain or sidechain-mainchain atom-atom distances for which an equivalent distance can be found in at least one of the reference proteins, MODELER applies a restraint to that distance in the model. Once again, these are described by a Gaussian distribution of the distance difference, similar to that used above for the mainchain Ca-Ca and N-O atom-atom distances.
The main-chain conformation classes for a residue can be described by the main-chain dihedral angles (f,y). As previously discussed, the third main-chain dihedral angle w is separately described by a bimodal Gaussian PDF for Pro residues and a monomodal Gaussian PDF for all others. The distribution of f,y pairs in the Brookhaven PDB is approximated by six distinct Gaussian peaks (Sali and Blundell 1993a) whose positions and widths are given in the table below.
These peaks correspond to six main-chain conformation classes: alpha helix (A), idealized beta strand (B), polyproline conformation (P), the positive f region accessible to Gly residues (G), left-handed alpha helix (L) and an extended conformation (E). If the probability wi that a restrained residue in the model is found in the main-chain conformation class i (i=A,B,P,G,L,E) is known, then the PDF restraining the dihedral angles f and y is given by a binomial function of the form:
| Eq. 23 |
|
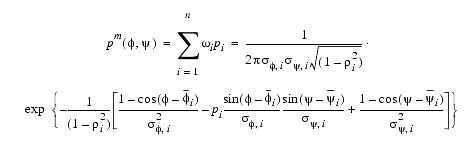
where p < 1. p is the correlation coefficient between f and y. Derivation of the probabilities wi used in the above expression depends upon which other features of the protein structure were found to correlate with the main-chain conformation class M. A careful study (Sali and Blundell 1993a) using the local protein database revealed that PDFs of the form 
were best suited for predicting wi. The variables involved are
R Residue type of the restrained residue.
M' Main-chain conformation class for equivalent residue in
reference protein with known structure.
s Residue neighborhood difference.
The residue neighborhood difference s is a value (typical range 0 to 2) that describes the dissimilarity between the residue-residue neighborhoods of two equivalent residues in an alignment. It is computed by the following scheme.
1. Find all neighbors of residue in structure A (cutoff distance 6.0 Å used).
2. Find equivalent residues in model (structure B) using the given sequence alignment.
3. Find sum of dissimilarity scores using a published matrix (Sali and Blundell 1990).
4. Add a gap penalty if there is a deletion in structure B.
The residue neighborhood difference(s) is then the total score divided by the number of neighbors found in structure A. If no neighbors were found in A, then this implies a score of zero. MODELER then uses the conditional PDF
to compute the probabilities wi needed to restrain the main-chain conformation class M via Eq. 23. Tests using known structures not involved in the fitting found this scheme to predict the main-chain conformation class with a success rate of approximately 73%. Allowing for swapping between the structurally similar B,P classes as well as between the L,G classes a prediction success of >87% was found (Sali and Blundell 1993a).
In a manner similar to that described above, the side-chain dihedral angles ci are restrained using a PDF that is a sum of Gaussians.
| Eq. 24 |
|
where wij is the probability that the restrained side-chain angle ci is in the class j and N[a,s] is a Gaussian PDF with mean a and standard deviation s. The dihedral angle ranges defining each class along with the class name, mean, and standard deviations are described in Table 12.
As the table shows, the side-chain conformation classes ci are dependent upon the residue type r. Thus, the simplest available PDF would be one of the form p(ci/r), which is equivalent to using a side-chain rotamer library (Ponder and Richards 1987).
All residue types except Val and Ser have c1 dihedral angles that most frequently fall into the "-" class. Val predominantly occupies the "t" class, while Ser is slightly more frequently found in the "+" class. A careful study of the effects of including various protein descriptors on the accuracy of predicting the c1 side-chain dihedral conformation class c1 has been performed (Sali and Blundell 1993a). Using the alignments database the optimum PDF for the prediction of the c1 class probability w1i, was found to be of the form p(c1,/r, c'1, r', s). Where r and c1 are the residue type and c1 class of the restrained residue in the model protein, r' and c'1 are the residue type and c1 class of an equivalent residue in a known reference protein, and s is the residue neighborhood difference described previously. This scheme was found to be most accurate in predicting the c1 conformation class of large buried residues such as Trp, Cys, Leu, Val, and Tyr where a prediction success of approximately 80% was found. It was least successful in predicting the c1 conformation class of smaller exposed residues such as Asn, Met, Arg, Glu, and Ser (approximately 50% successful).
Residues having a trimodal c2 distribution (Asp, Ile, Lys, Leu, Met, Gln, and Arg) prefer the "t" class. Trp is most frequently found in class 1 while His and Asn are most frequently found in class 2. In attempting to predict the c2 dihedral angle class c2 for a given residue in the protein model, the simplest PDF type p(c2/r) was found to have a 70.7% success rate. Taking into account the residue type r' and the c1 and c2 dihedral angle classes c'1 and c'2 found in an equivalent PDF leads to a PDF of the form p(c2/r, r', c'1, c'2) with a slightly improved prediction success rate of 72.3%. The latter has been used for computing the probabilities w2j required to restrain c2 dihedral angles.
Glu residues occupy two c3 classes, of which class 2 is predominant. The residues Met, Cys, Arg, and Gln occupy three c3 classes; Met and Gln have near equal populations for the three classes: Arg occupies the t class in 47% of cases, while Lys does so in 71% of cases. The simplest PDF form p(C3/r) has a c3 class prediction (c3) success rate of 58.5%. A slight improvement was found when using a PDF of the form p(c3/r,c3',r',t) where c3' is the c3 class of an equivalent residue and t is the main-chain secondary structure class of the model protein. The latter PDF form is used in computing c3 class probabilities w3, for use in restraining these dihedral angles via Eq. 24. The prediction success rates based on these PDFs alone are shown below.
(°)
|
|||||
|---|---|---|---|---|---|
The only standard residues having a c4 side-chain are Arg and Lys. These were found to occupy the t class in 64% and 74% of cases respectively. The prediction success rate of the simplest PDF p(c4/r) is 75.3%. This form is used for computing probabilities w4j for restraining c4 dihedral angles using Eq. 24.
A feature f of a protein structure is any geometric descriptor associated with a set of atoms i,j,k,l...; examples of protein features are a distance between two atoms i,j and a bond angle formed by three atoms i,j,k. The probability density functions (PDFs) described in previous sections are basis PDFs pf(f) and are derived from a single homologous structure. In general, a single feature in a model protein structure can be restrained by several basis PDFs pfk(f) k=1,2,3..., where k is the index of the homologous structures. A feature PDF pF(f) then combines together all appropriate basis PDFs that are needed to describe the feature f. The lower- and uppercase superscripts thus relate to the basis and feature PDFs respectively.
As an example when a certain Ca-Ca distance d in a model protein sequence is to be restrained using two homologous reference proteins then there are two basis PDFs. If the equivalent Ca-Ca distances in the reference proteins are d' and d", then the basis PDFs are of the form p(d/d') and p(d/d''). These can be combined as a weighted sum to form a PDF that is conditional on both of the reference distances d' and d''.
| Eq. 25 |
|
The weighting factors 
and 
are functions of the average residue neighborhood differences 
and 
between the model protein and each of the reference proteins. The functional form of the weighting factors w(s) is:
| Eq. 26 |
|
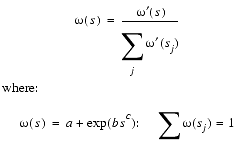
The sum j runs over all reference proteins and a,b,c are constants found by a least squares analysis using all possible alignments of three proteins in the alignments database. The effect of these weighting functions is that the contribution that a related structure makes to a 3D model falls faster than linearly with respect to the average residue neighborhood difference between the modeled and reference protein. This provides the mechanism by which the local sequence similarity between the reference and the model proteins may be applied differently in different regions of the model fold. Since the atoms involved in the Ca-Ca distance must also obey the van der Waals restraints, the Ca-Ca conditional PDF is multiplied by a van der Waals basis PDF to yield the final feature PDF.
| Eq. 27 |
|
This method of taking a weighted sum is then used for combining any number of basis PDFs of the same type. When generating feature PDFs for features such as main-chain and side-chain conformation, the average residue neighborhood difference 
is replaced by the residue neighborhood difference s.
A description of the form of the feature PDFs is now given, where the right hand side of each expression contains the basis PDFs that have already been discussed. The variables a,b,c... are the features of the reference structures that are used in deriving the appropriate basis PDFs; the subscript i refers to each reference protein contained in the alignment with the sequence of the model protein, and the weights wi are derived from Eq. 26.
Ca-Ca distance feature PDF
Main-chain N-O distance feature PDF
Stereochemical feature PDF
Main-chain conformation feature PDFs
Side-chain dihedral angle feature PDFs
Molecular PDF used for structure generation
The feature PDF used to restrain Ca-Ca distances (d) in the model protein is of the form:
| Eq. 28 |
|
This PDF is computed for all Ca-Ca atom pairs in the model protein that have at least one equivalent distance in the known reference proteins less than a cutoff distance (20 Å) and where the two residues in the model are not adjacent in the sequence. The summation is over all reference structures having an equivalent Ca-Ca distance.
A distance (h) between main-chain N and O atoms is restrained by a feature PDF of the form:
| Eq. 29 |
|
This is evaluated for all N-O distances in the protein model that have at least one equivalent distance in the reference proteins less than a cutoff (10 Å) and where there are at least two intervening residues. As above the sum runs over all known structures having an equivalent N-O pair present.
The PDF form used to restrain a stereochemical feature (e) such as a bond length, bond angle, dihedral angle, or van der Waals contact is simply equal to the basis PDF:
| Eq. 30 |
|
The feature PDF pV(v) restrains only those pairs of atoms not already restrained by a bond length, bond angle, or dihedral feature PDF.
The main-chain conformation in the model protein is restrained by a feature PDF of the form:
| Eq. 31 |
|
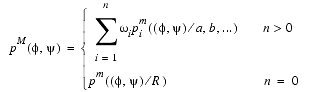
If there is no equivalent residue in any of the known structures (n = 0) then the PDF depends only on the residue type. If there are equivalent residues (n > 0) then the feature PDF is a weighted sum of basis PDFs.
The side-chain dihedral angles c1, c2, c3, and c4 are restrained by feature PDFs of the form:
| Eq. 32 |
|
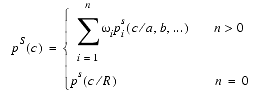
where c stands for either c1, c2, c3, or c4. In the case of no equivalent residues in the known structures (n = 0), a rotamer library based on the residue type is used; when equivalent residues are present (n > 0), then the feature PDF is again a weighted sum of basis PDFs.
The objective function used for structure generation in MODELER is referred to as a molecular PDF. This is a combination of all the feature PDFs pF(fi) used to restrain particular geometric features (fi) of the protein model. We seek the 3D protein model that is consistent with the most probable values of the individual features. The feature PDFs measure the probability of occurrence for the values of a single feature. The molecular PDF then measures the probability of occurrence for values adopted by several features simultaneously.
If the feature PDFs are assumed to be independent, then the molecular PDF is simply a product of feature PDFs described above:
| Eq. 33 |
|
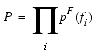
Finding a maximum for P leads to the most probable 3D model given the alignment of the sequence of the model with those of the known proteins. The assumption of the independence of the feature PDFs is equivalent to describing the system by a molecular energy function that is a sum of terms due to each feature PDF.
The previous sections describe the procedures used to derive basis PDFs from a local protein database and to compute the feature PDFs and molecular PDF for a model protein structure. The objective function (F) that is optimized by MODELER is the natural logarithm of the molecular PDF.
| Eq. 34 |
|
Minimizing F corresponds to maximizing P but has advantages in terms of avoiding floating-point overflow issues. The optimization takes place in two distinct stages. The first is a Cartesian space variable target function (VTF) conjugate gradient optimization. The optimum of the MODELER PDF is sought by a series of target functions that eventually equals the full molecular PDF. The series starts only with sequentially local restraints, adding longer range restraints as the calculation proceeds, until all restraints are being used and the full molecular PDF is calculated. The optional second optimization stage consists of a restrained molecular dynamics (MD) simulated annealing scheme. See Figure 2 below.
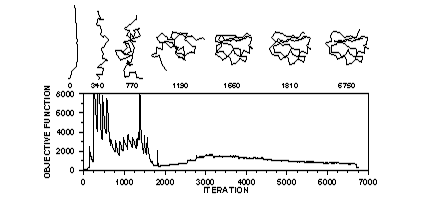
Figure 2. Optimization of the objective function for a linear starting model
Optimization of the objective function (curve) starts with a random or distorted template structure. The iteration number is indicated below each sample structure. The first ~2,000 iterations correspond to the variable target function method relying on the conjugate gradients technique. This approach first satisfies sequentially local restraints and slowly introduces longer range restraints until the complete objective function is optimized. In the last 4,750 iterations, molecular dynamics with simulated annealing is used to refine the model.
The starting conformations used by MODELER are generated by the following scheme.
1. First superpose all templates on the first template using the Ca atoms and the given alignment. Each atom in the modeled protein having an equivalent atom in at least one of the templates has coordinates that are the mean of the coordinates for the template atoms. The remaining undefined atoms have their coordinates set by using internal coordinates derived from a CHARMm residue topology library.
2. Next, a random coordinate shift (default between ± 4 Å) is added to each atomic position. This scheme generates starting models similar to the templates for faster convergence.
For the parts of the model sequence which are not aligned to any template structures, no homology restraints, such as Ca-Ca distance restraints, can be applied. During model generation, those parts of the model structure are optimized according to CHARMm-derived stereochemical and non-bonded restraints, as well as statistical preferences of the different residue types for the different regions of the Ramachandran plot and for the different sidechain rotamers. Those parts of the structure generally have larger errors compared to the regions which are modeled based on a template structure. Sometimes, it is desirable to refine the loop conformation after model generation using a statistical pair potential by a more extensive molecular dynamics/simulated annealing procedure. This section discusses the energy function used by loop optimization.
Loops can be defined automatically from the model to template sequence alignment. Any part of the model sequence not aligned with a template structure is defined in MODELER as a loop. You can also specify loops as any sequence segment. During loop optimization, all the atoms are fixed except those defined in the loop region.
| Eq. 35 |
|
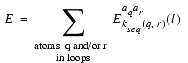
is a sum of the pairwise interactions between loop atoms and the rest of the protein. Those interactions are calculated using the statistical energy derived from pairwise atomic interactions in known protein structures using the Boltzmann approximation (Melo and Feytmans 1997). The energy term is dependent on the stereochemical type of atoms. aq and ar represent the number of peptide bonds (sequence separation), kseq(q,r), and class l of the distance between them.
Each pairwise potential Ekij(l) is derived from the statistics of atom type pairs in known protein structures:
| Eq. 36 |
|
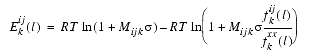
where Mijk is the number of observations for the atom-type pair ij at the sequence separation k corresponding to:
| Eq. 37 |
|
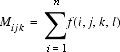
s (=1/50) represents the weight given to each observation.
fkij(l) is the relative frequency of occurrence for the atomic pair ij at sequence separation k in the class of distance l:
| Eq. 38 |
|
fkxx(l) is the relative frequency of occurrence for all the atomic pairs at sequence separation k in the class of distance l:
| Eq. 39 |
|
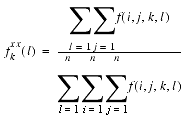
The same method and energy function are used to optimize a mutant structure. One or more residues can be selected for mutations from a known protein structure and the structure of the mutant is optimized using the loop optimization protocol. All atoms within a defined distance to the mutated residue are optimized.
Bernstein, F.C.; T.F.Koetzle, G.J.B.Williams, E.F.Meyer Jr, M.D.Brice, J.R.Rodgers, O.Kennard, T.Schimanouchi, M.Tasumi, "The protein data bank: A computer based archival file for macromolecular structures," J.Mol. Biol. 112 535-542 (1977).
Blundell, T. L.; B. L. Sibanda; M. J. E. Sternberg; J. M. Thornton "Knowledge-based prediction of protein structures and the design of novel molecules" Nature (London) 326 347-352 (1987).
Blundell, T. L.; D. Carney; S. Gardner; F. Hayes; B. Howlin: T. Hubbard; J. Overinton; D. A. Singh; B. L. Sibanda; M. Sutcliff "Knowledge-based protein modeling and design" Eur. J. Biochem. 172 513 (1988).
Browne, W. J.; A.C.T. North; D.C. Phillips; K. Brew; T. C. Vanaman; R.C. Hill "A possible three-dimensional structure of bovine -lactalbumin based on that of hen's egg-white lysozyme" J. Mol. Biol. 42 65-86 (1969).
Braun, W. and N. Go "Calculation of protein conformations by proton-proton distance constraints: A new efficient algorithm" J. Mol. Biol. 186 611-626 (1985).
Brooks, B.R.; R.E. Bruccoleri, B.D. Olafson, D.J. States, S. Swaminathan, M.Karplus, J.Comp.Chem. 4 187 (1983)
Greer, J. "Model for haptoglobin heavy chain based upon structural homology" Proc. Nat. Acad. Sc. U.S.A. 77 3393 (1980).
Greer, J. "Comparative model-building of the mammalian serine proteases" J. Mol. Biol. 153 1027-1042 (1981).
Greer, J. "Model structure for the Inflammatory Protein C5a" Science 228 1055 (1985).
Matsumoto, R., A. Sali, N. Ghildyal, M. Karplus, R. L. Stevens "Packaging of proteases and proteoglycans in the granules of mast cells and other hematopoietic cells" J. Biol. Chem. 270 19524- 19531 (1995).
Melo, F. & Feytmans, E. "Novel knowledge-based mean force potential at the atomic level" J. Mol. Biol. 267 207-222 (1997).
Nilsson, L.; M. Karplus, J. Comp. Chem. 7 591 (1986).
Ponder, Richards, J.Mol. Biol. 194 775-791 (1987).
Sali, A. "Modeling mutations and homologous proteins," Curr. Opin. Biotech. 6 437-451 (1995a).
Sali, A. "Protein modeling by satisfaction of spatial restraints" Molecular Medicine Today 1 270-277 (1995b).
Sali, A.; T.L. Blundell, "Definition of general topological equivalence in protein structures: A procedure involving comparison of properties and relationships through simulated annealing and dynamic programming," J. Mol. Biol. 212 403-428 (1990).
Sali, A.; T.L. Blundell, "Comparative protein modeling by satisfaction of spatial restraints," Mol. Biol. 234 779-815 (1993a).
Sali, A.; R. Matsumoto, H.P. McNeil, M. Karplus, R.L. Stevens, "Three-dimensional models of four mouse mast cell chymases. Identification of proteoglycan-binding regions and protease-specific antigenic epitopes," J. Biol. Chem. 268 9023-9034 (1993b).
Sali, A.; J.P. Overington, "Derivation of rules for comparative protein modeling from a database of protein structure alignments," Protein Sci. 31 582-1596 (1994).
Sali, A.; L. Pottertone, F. Yuan, H. van Vlijmen and M. Karplus "Evaluation of comparative protein modeling by MODELLER" Proteins 23 318-326 (1995).
Shotton, D. M.; H. C. Watson "Three-dimensional Structure of Tosyl-elastase" Nature 225 811 (1970).
and 
are shown.